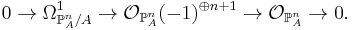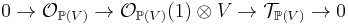Euler sequence
In mathematics, the Euler sequence is a particular exact sequence of sheaves on n-dimensional projective space over a ring. It shows that the sheaf of relative differentials is stably isomorphic to an (n + 1)-fold sum of the dual of the Serre twisting sheaf.
Contents |
Statement
For A a ring, there is an exact sequence of sheaves
It can be proved by defining a homomorphism 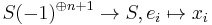 with
with ![S = A[x_0,\ldots,x_n]](/2012-wikipedia_en_all_nopic_01_2012/I/71c84fd76a8e6a17b251378bb8a0960a.png) and
and 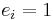 in degree 1, surjective in degrees
in degree 1, surjective in degrees 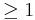 and checking that locally on the n + 1 standard charts the kernel is isomorphic to the relative differential module.[1]
and checking that locally on the n + 1 standard charts the kernel is isomorphic to the relative differential module.[1]
Geometric interpretation
We assume that A is a field k.
The exact sequence above is equivalent the sequence
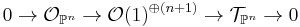 .
.
We consider V a n+1 dimensional vector space over k , and explain the exact sequence
This sequence is most easily understood by interpreting the central term as the sheaf of 1-homogeneous vector fields on the vector space V. There exists a remarkable section of this sheaf, the Euler vector field tautologically defined by associating to a point of the vector space the identically associated tangent vector (ie. itself : it is the identity map seen as a vector field).
This vector field is radial in the sense that it vanishes uniformly on 0-homogeneous functions, that is, the functions that are invariant by homothetic rescaling, or "independent of the radial coordinate".
A function (defined on some open set) on  gives rise to a 0-homogeneous function V (again partially defined). We obtain 1-homogeneous vector fields by multiplying the Euler vector field by such functions. This is the definition of the first map, and its injectivity is immediate.
gives rise to a 0-homogeneous function V (again partially defined). We obtain 1-homogeneous vector fields by multiplying the Euler vector field by such functions. This is the definition of the first map, and its injectivity is immediate.
The second map is related to the notion of derivation, equivalent to that of vector field. Recall that a vector field on an open set U of the projective space  can be defined as a derivation of the functions defined on this open set. Pulled-back in V, this is equivalent to a derivation on the preimage of U that preserves 0-homogeneous functions. Any vector field on
can be defined as a derivation of the functions defined on this open set. Pulled-back in V, this is equivalent to a derivation on the preimage of U that preserves 0-homogeneous functions. Any vector field on 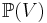 can be thus obtained, and the defect of injectivity of this mapping consists precisely of the radial vector fields.
can be thus obtained, and the defect of injectivity of this mapping consists precisely of the radial vector fields.
We see therefore that the kernel of the second morphism identifies with the range of the first one.
The canonical line bundle of projective spaces
By taking the highest exterior power, one gets that the canonical sheaf of a projective space is given by
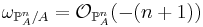 .
.
In particular, projective spaces are Fano varieties, because the canonical bundle is anti-ample and this line bundle has no non-zero global sections, so the geometric genus is 0.
Notes
- ^ Theorem II.8.13 in Hartshorne 1977
References
- Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR0463157